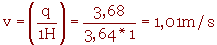Enoncé
A un nouveau recrue, on demande de calculer une chambre de sédimentation. Cette chambre de sédimentation est destinée à retenir des particules de fer issues d'une fonderie.
On vous donne :
- dp =35 µm (supposé valeur constante, pas de distribution)
- gaz : air ambiant
- q=3,68 m3/s
- vitesse de sortie : v=3 m/s
- ρp = 7620 kg.m-3
Correction
K = 2,28 < 3,3 on est donc en régime de Stokes et 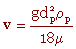
L'aire de collecte de particule de fer est L.l (longueur * largeur)
Partant de l'expression de la vitesse, on tire l'expression du diamètre puis on remplace cette vitesse par le rapport débit volumique q sur la section de passage L*l.
On obtient : 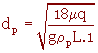
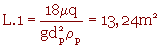
La section droite pour v=3 m/s est l.H=q/v=1,22 m2 (H : hauteur)
H est généralement = 1 m
Donc l=1,22 m et L=10,85 m
D'où le volume de la chambre de sédimentation V=L.l.H=13,24 m3.
La plupart des chambre de sédimentation ont un e forme cubique (tout comme les filtres électrostatiques) d'où 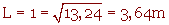 .
.
Dans ce cas, la vitesse du gaz sera :