3.2.3.1. Définitions
Pendant le temps Δt l'augmentation du volume de
filtrat est ΔV. Le débit instantané de filtrat est
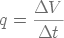 (9)
(9)
Si
Ω est la surface filtrante, la vitesse débitante en fût vide est :
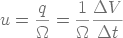 (10)
(10)
Hypothèses
- Le régime d'écoulement à travers le gâteau est laminaire.
- Le gâteau est homogène et incompressible.
Les vitesses absolues de filtration sont toujours très faibles et l'expérience
montre (a posteriori) que le fluide s'écoule en régime laminaire dans
les pores.
Par exemple, le débit de filtrat à travers un gâteau de résistance moyenne est de
l'ordre de 2,5 m3 / m2·h,
soit une vitesse u de l'ordre de 0,07 cm/s.
Si l'on admet que la dimension des grains formant le gâteau est bien inférieur à
25 µm, on peut calculer que pour un liquide dont
la masse volumique et la viscosité sont voisines de celle de l'eau.
Le nombre de Reynolds est inférieur à 0,01.
Dans ces conditions, on observe que la perte de charge est proportionnelle au
débit instantané et à la viscosité du fluide :
ΔP = ηu
(11)
Le coefficient de proportionnalité est une « résistance » à l'écoulement par
unité de surface qui a la dimension L-1.
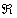 est la somme de deux résistances en série :
celle du support Rs et celle du gâteau en cours
de formation R
est la somme de deux résistances en série :
celle du support Rs et celle du gâteau en cours
de formation R
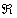 = R + Rs
(12)
= R + Rs
(12)
3.2.3.2. Résistance du support
Le choix du support réalise un compromis entre une résistance Rs
minimale et une dimension des pores suffisamment petite pour arrêter les particules. Comme cette
dimension est liée à la taille des grains formant le gâteau, il peut être intéressant de calculer
l'épaisseur équivalente du gâteau ayant la même résistance que le support. Il est possible de trouver
des supports satisfaisants dont l'épaisseur équivalente correspond à 0,25 mm,
ce qui est vite négligeable devant l'épaisseur du gâteau. Le tableau 1 donne quelques valeurs de
Rs.
| Type de toiles |
Ouverture (µm) |
Rs (m-1) |
| Toiles métalliques REPPS inox |
350 |
1·107 |
| 47 |
2·107 |
| 5 |
2·108 |
| Tissus coton croisé |
|
9·107 à 5·108 |
| nylon mono filament |
1·106 à 5·106 |
| nylon multi filament |
2·106 à 3·108 |
| verre |
6·107 à 7·108 |
| Non tissé |
|
6·106 à 3·109 |
3.2.3.3. Résistance spécifique du gâteau α
Écrivons que la résistance à l'écoulement par unité de surface du gâteau est
proportionnelle à la masse de matériau séché déposé par unité de surface filtrante :
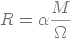 (13)
(13)
Cette relation constitue une définition de la grandeur α qui
porte le nom de « résistance spécifique du gâteau ». Le fait de supposer
α constant revient à admettre que le gâteau se dépose régulièrement
et que sa texture reste la même pendant toute la filtration ; autrement dit, nous faisons
l'hypothèse d'un gâteau homogène et incompressible.
La dimension de α est : LM-1.
Cherchons à exprimer la résistance spécifique α du gâteau
en fonction de sa perméabilité B définie par l'équation de Darcy :
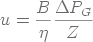 (14)
(14)
ΔPG = P2 - P1
est la chute de pression à l'intérieur du gâteau. Elle peut aussi être calculée à partir de
l'équation :
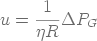
d'où
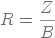 (15)
(15)
Explicitons la masse M du gâteau, d'épaisseur Z :
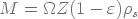
ρs : masse volumique du matériau constituant le lit.
Il vient :
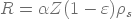 (16)
(16)
d'où
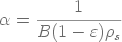 (17)
(17)
Ordre de grandeurs de α
| talc (pression de filtration ∼ 3 bar) |
α ≈ 4,7·1011 m·kg-1 |
| Diatomite naturelle |
α ≈ 6·1010 m·kg-1 |
| Diatomite calcinée |
6·109 < α < 6·1010 m·kg-1 |
| Diatomite calcinée frittée |
6·108 < α < 6·109 m·kg-1 |
| billes de verre (ρs = 2750 kg·m-3,
ε = 0,40) : |
|
| diamètre en μm |
500 |
100 |
20 |
5 |
| α en m·kg-1 |
2,2·106 |
5,5·107 |
1,38·109 |
2,2·1010 |
|
3.2.3.4. Expressions de la vitesse de filtration
Reprenons les relations (1) et (2) :
ΔP = (Rs + R)ηu.
En y substituant la valeur de la résistance à l'écoulement par unité de surface du gâteau :
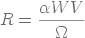 (18)
(18)
ainsi que celle de la vitesse d'écoulement :
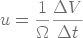
on obtient une équation hyperbolique :
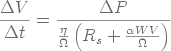
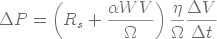 (19)
(19)
Liant la chute de pression, le débit instantané
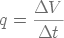 et le volume de filtrat V (voir figure 3) :
et le volume de filtrat V (voir figure 3) :
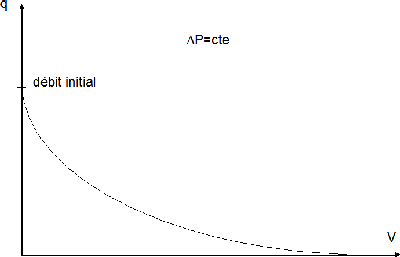
Figure 3 : q = ƒ(V).

