C'est le cas des filtres sous vide et de certaines filtrations sous pression.
L'intégration de l'équation (10) avec
ΔP = Cte donne
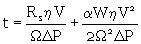 (21)
(21)
En supposant V = 0 pour t = 0.
On pourrait représenter le volume du filtrat (figure 4), en fonction du temps, mais le diagramme
n'est pas pratique, d'abords parce qu'il ne donne pas une fonction linéaire et ensuite parce que la pente
initiale peut être très grande (Rs est petit) et donc difficile à
déterminer. Il est plus pratique de porter t/V en fonction de
V, soit :
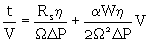 (22)
(22)
Avec cette représentation utilisée pour la détermination expérimentale des résistances
spécifiques du support et du gâteau, les points expérimentaux (figure 5) devront donc
s'aligner sur une droite dont l'ordonnée à l'origine « b »
est proportionnelle à la résistance du support et la pente « a »
est proportionnelle à la résistance spécifique du gâteau.
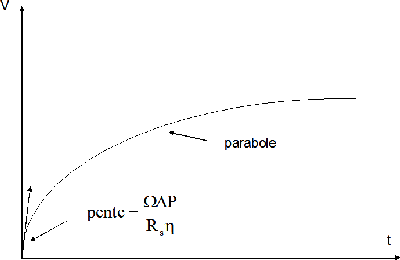
Figure 4 : V = ƒ(t)
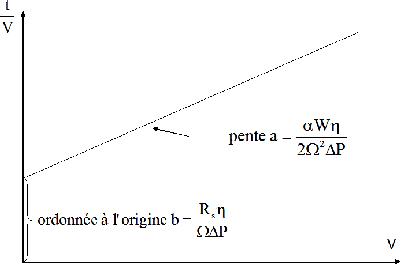
Figure 5 : (t/V) = ƒ(V)
Remarque
En réalité, la résistance spécifique étant souvent très faible et la perte de
charge
ΔP non stabilisée dans les premiers
instants de la filtration, l'ordonnée à l'origine n'est pas exploitable.
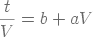 (23)
(23)
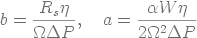 (24)
(24)

