Exercice 3.1
Au cours d'une filtration pilote sur filtre à tambour rotatif sous vide, on veut déterminer la porosité du gâteau.
On prélève 2 kg de gâteau saturé en jus-mère à la sortie de l'auge. Après séchage en étuve, ce prélèvement ne pèse plus que 1,328 kg. Sachant que les masses volumiques du bicarbonate et du jus-mère sont respectivement 2 220 kg.m-3 et 1 127 kg.m-3, déterminer la porosité du gâteau en fin de filtration.
Remarque : On assimilera le jus-mère à une solution aqueuse de NaCl, la densité de la solution est donnée dans le tableau ci-dessous.
| Titre massique de NaCl |
Densité |
| 0,16 |
1,124 |
| 0,20 |
1,157 |
Exercice 3.2
Sachant que la porosité du gâteau de bicarbonate est 0,57, calculer le rapport d'humidité et la siccité du gâteau avant essorage sous vide.
Exercice 3.3
Sachant que la teneur de la suspension de bicarbonate est de 0,257 kg/kg de suspension, calculer la masse de bicarbonate sec obtenu, ainsi que le liquide retenu dans le gâteau pour 1m3 de filtrat.
Exercice 3.4
Exprimer le rapport entre le volume interstitiel de liquide qui reste emprisonné dans le gâteau et le volume de filtrat.
Application numérique:
m = 1,67 ; s1 = 10-3 ; s2 = 10-2 ; s3 = 10-1 ; s = 2.10-1
Exercice 3.5
Dans une filtration discontinue, la durée du cycle et le volume de filtrat correspondant sont limités par l'épaisseur maximale que peut atteindre le gâteau par suite de la conception géométrique du filtre. Soit ZM cette épaisseur limite, calculer pour les concentrations de l'exercice précédent, le volume de filtrat récupérable par m2 de surface filtrante.
On prendra : ρ
1 = 1 127 kg.m
-3 ; ρ
s = 2 220 kg.m
-3 ; ε = 0,57 : Z
M = 2 cm
Exercice 3.6
Calculer la vitesse et le nombre REYNOLDS de pores correspondant à un débit de 2,5m3.h-1.m-2 à travers un gâteau formé de grains de diamètre équivalent 25 mm.
Masse volumique et viscosité du liquide : ρ = 103 kg.m-3 ; h = 10-3 Pl
Porosité du gâteau : ε = 0,5
Exercice 3.7
Dans l'exemple précédent, calculer la résistance de l'unité de surface de support équivalente à 0,25 mm de gâteau.
Exercice 3.8
Dans l'exemple précédent, le gâteau formé sur le support a une épaisseur Z = 4 cm. Calculer :
1) La résistance du gâteau par unité de surface
2) La masse de gâteau anhydre par m2 de support. Masse volumique du solide : ρs = 2,5.103 kg.m-3
3) La résistance spécifique du gâteau.
Exercice 3.9
Une suspension de teneur s = 10-2 kg de solide/kg de suspension est filtrée sous une pression constante ΔP = 2 bars. Le gâteau obtenu a une rapport d'humidité m = 1,40 et une résistance spécifique α = 4,15.10 8 m.kg-1. La résistance du support filtrant est Rs = 1,3.10 8.m-1.
Calculer le débit instantané par m2 de filtre correspondant à l'obtention de V m3 de filtrat/m2 de surface filtrante.
Application numérique : V = 0 , 1 , 2 , 3 , 4 m3
La viscosité et la masse volumique du filtrat sont respectivement :
η = 10
-3 Pa.s ; ρ
1 = 10
3 kg.m
-3
Exercice 3.10
Les données concernant la filtration d'une suspension aqueuse de talc sont :
| liquide |
ρ1= 1 000 kg.m-3 |
η = 10-3 Pa.s |
| solide |
ρs = 2 700 kg.m-3 |
s = 0,03 |
| support |
Rs = 7,5.1010 m-1 |
Ω = 1 m2 |
| gâteau |
α = 4,3.1011 m.kg-1 |
m ~ 2,5 |
| pression |
ΔP = 3,5 bars = 3,5.105 Pascals |
|
Calculer les paramètres a et b de l'équation (23) (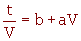 ) et en déduire le temps nécessaire à l'obtention d'un gâteau de 6 cm d'épaisseur.
) et en déduire le temps nécessaire à l'obtention d'un gâteau de 6 cm d'épaisseur.
Exercice 3.11
Une suspension diluée donne un gâteau compressible de résistance spécifique α = 108 m.kg-1 sous 0,5 bar de pression de filtration. Le coefficient de compressibilité est η = 0,8. Sachant que sous 0,5 bar on obtient 10 m3 pendant la première heure de filtration, calculer le temps nécessaire pour obtenir 10 m3 avec une pression de filtration de 2 bars.
On supposera que la loi de variation de la résistance spécifique en fonction de ΔPest de la forme :
α = α0ΔPn
et que la résistance du support est négligeable.
Exercice 3.12
Les données concernant la filtration du bicarbonate dans les soudières sur filtre rotatif sous vide sont :
| eaux mères |
ρ1 = 1 127 kg.m-3
η = 1,35.10-3 Pa.s
|
|
| bicarbonate |
ρs = 2 220 kg.m-3 |
|
| suspension |
s = 0,257 |
|
| gâteau |
ε ~ 0,57 |
α inconnue |
| support |
S = 14,4 m2 |
Rs négligée |
| filtre |
N = 5 t/mn
ΔP = 0,49 bar |
Ψ = 0,106 |
| débit bicarbonate sec |
Wq = 19,5 kg.s-1 |
|
Calculer la résistance spécifique et l'épaisseur du gâteau formé.
Exercice 3.13
Pourquoi les procédés de coagulation et de floculation doivent-ils nécessairement précéder un filtre rapide ?
Exercice 3.14
Expliquez comment on peut mesurer une perte de charge de 2 m à travers un filtre à sable rapide alors que la hauteur d'eau au-dessus du milieu filtrant n'est que de 1 m.
Exercice 3.15
On se propose de remplacer la totalité du sable d'un filtre à sable rapide par de l'anthracite. Vérifiez si ce choix est réaliste : dans un premier temps, déterminez quelles sont les données requises pour effectuer une telle évaluation (mesures à faire sur le filtre existant) ; dans un deuxième temps, indiquez comment vous utiliserez ces données.
Exercice 3.16
En utilisant l'équation de Rose, calculez la perte de charge initiale à travers un filtre à sable rapide de 50 cm d'épaisseur. La porosité du matériau filtrant est de 0,42, la température de l'eau, de 15°C, et la charge superficielle, de 4,9 m/h.
L'analyse granulométrique a donné les résultats présentés ci-dessous.
N° de tamis
|
Pourcentage retenu |
Diamètre moyen* (mm) |
28 – 32
32 – 35
35 – 42
42 - 48 |
15,70
30,50
38,42
15,38
|
0,54
0,46
0,38
0,32 |
| *moyenne géométrique |
Le milieu filtrant n'est pas stratifié. Supposez que les grains de sable sont des sphères parfaites.
Exercice 3.17
En utilisant l'équation de Carman-Kozeny, calculez la perte de charge initiale à travers un filtre à sable rapide de 60 cm d'épaisseur. La porosité du matériau filtrant est de 0,40, la température de l'eau, de 4°C. et la charge superficielle, de 4,0 m/h. L'analyse granulométrique a donné les résultats présentés ci-dessous.
N° de tamis |
Pourcentage retenu |
Diamètre moyen* (mm) |
28 – 32
32 – 35
35 – 42
42 - 48 |
22,00
38,00
30,00
10,00
|
0,54
0,46
0,38
0,32 |
| *moyenne géométrique |
Le milieu filtrant est stratifié. Supposez que les grains de sable sont des sphères parfaites.
Exercice 3.18
On se propose de remplacer les 75 cm de sable d'un filtre à sable rapide par 75 cm d'anthracite (densité relative: 1.5 ; porosité: 0,5). L'analyse granulométrique de l'anthracite a donné les résultats présentés ci-dessous.
N° de tamis (US standard) |
Diamètres (mm) |
Pourcentage retenu par chaque tamis |
8
16
20
30
100 |
2,38
1,19
0,84
0,59
0,149
|
0,00
66,50
21,50
11,00
1,00 |
Lorsque le filtre est au repos, les crêtes des goulot tes sont situées à 70 cm au-dessus du milieu filtrant. La surface de filtration est de 50 m 2 et le débit de la pompe de lavage, de 500 L/s.
-
Peut-on laver les filtres à anthracite sans perdre une certaine quantité de milieu filtrant?
-
Quelles doivent être les caractéristiques du floc pour que le rendement du filtre à anthracite soit acceptable ?

